Triton 学习手记（一）：基本概念

前言

什么是 Triton？ Triton 的官网文档中是这样介绍的：

Triton is a language and compiler for parallel programming. It aims to provide a Python-based programming environment for productively writing custom DNN compute kernels capable of running at maximal throughput on modern GPU hardware.

简单来说 Triton 是一个允许你在 Python 中以 Python 风格的代码来写 GPU 并行计算程序的包。

我们知道在神经网络经常涉及大量的运算，其中有非常多的运算是可以并行处理的。例如，对一个 $1024 \times 1024$ 的矩阵进行 ReLU 运算。由于 ReLU 运算对每个元素都是独立的，因此我们可以将这个矩阵切分为数个小的矩阵，然后并行地对这些小矩阵进行 ReLU 运算，从而加速整个运算。事实上 pytorch、tensorflow 等深度学习框架所提供的函数的背后都或多或少使用了 CUDA 及其类似的技术来实现并行加速。

然而这些函数并行化细节对用户隐藏，用户只能使用这些函数，而不能控制并行化细节。假设我们现在构思出了一个全新的函数，我们希望并行优化这个函数，但是这个函数又不是 pytorch 或 tensorflow 中的函数，我们该怎么办？这时候 Triton 就派上用场了。他提供了一个相对简单的语言（Python + 类 numpy 的语法），让用户可以在这个语言中控制 GPU 的并行化和运算细节，充分挖掘 GPU 的潜力。

这篇 Blog 是我学习 Triton 的笔记。作为初学者，我不可避免地会犯一些错误，欢迎大家指正。

单程序多数据

第一个概念是单程序多数据。

Triton 使用单程序多数据（Single Program Multiple Data, SPMD）的编程模型。也就是说在并发的时候，在同一时间运行的是同一份程序。这份代码在运行时通过某些系统提供的标识符来区分自己要处理哪份数据。

在 Triton 中，这份程序通常被称作 kernel。下面是一个简单的例子：

import triton.language as tl # 简单起见我们利用 `tl` 来指代 `triton.language` 模块
import triton
import torch

## 修饰符，表示这是一个 Triton Kernel
@triton.jit
def zero_kernel(x_ptr):
    # 获取当前程序的编号
    pid = tl.program_id(0)
    # 将当前程序的编号对应的元素设置为 0
    offset = pid
    tl.store(x_ptr + offset, 0)

if __name__ == "__main__":
    n = 128
    # 创建一个长度为 n 的空 tensor，并将其移动到 GPU 上
    x = torch.empty(n).to("cuda")
    print(x) # 打印未初始化前的 x
    grid = (n, )
    zero_kernel[grid](x)
    print(x) # 打印初始化后的 x

这个例子展示了 SPMD 的核心思想：在运行时，调度程序会根据 grid 启动 $n$ 个 zero_kernel，第 $i$ 个实例通过 tl.program_id(0) 知道自己的编号是 $i$，然后去设置第 $i$ 个元素。

如果觉得还是很难理解，我们不妨换个思路：

@triton.jit                         #
def zero_kernel(x_ptr):             # def zero(x, pid):
    pid = tl.program_id(0)          #
    pass                            #     pass

if __name__ == "__main__":          # if __name__ == "__main__":
    n = 128                         #     n = 128
    x = torch.empty(n).to("cuda")   #     x = torch.empty(n).to("cuda")
    grid = (n, )                    #     for pid in range(n):
    zero_kernel[grid](x)            #         zero(x, pid)

我们还是依照单线程循环的思路来写代码，只不过在 Triton 中，编译器自动根据 grid 来帮我们执行了“循环”。

Triton 允许我们设置最多三维的 grid，例如：

grid = (n, m, l)                    # for pid_n in range(n):
                                    #     for pid_m in range(m):
                                    #         for pid_l in range(l):
kernel[grid](*args)                 #             func(*args, pid_n, pid_m, pid_l)

注：调研了一些资料，目前暂时没有找到 grid 维度设置的最佳实践，似乎高维只是为了方便用户理解。

Tensor 的读取和存储

在阅读前面的zero-kernel时，你可能已经注意到，在zero函数中，我们向 zero_kernel 传递了一个 tensor，但是为什么 zero_kernel 的参数是 x_ptr？为什么 x_ptr + offset 表示第 offset 个元素？为什么不是像 Pytorch 那样直接使用 x[offset]？

指针

和 Pytorch 编程不太一样，Tensor 是以指针的形式传递给 Triton Kernel 的。这一设计的初衷是为了方便用户可以更精确地控制读取哪些元素。

我们可以把显存理解为一个巨大的一维数组，而指针是这个数组中的一个索引。类似索引，我们可以通过对指针加上或者减去一个整数来访问显存中的不同位置。

在正式介绍 Triton 中的 Tensor 的读取和存储之前，我们先来介绍一些前置的知识。如果读者对 Tensor 是如何在显存中布局的已经很熟悉，同时也了解 Strides 的含义，可以直接跳过下面两个小节。

Tensor 在显存中的布局

当我们新建一个 Tensor 时，无论这个 Tensor 是几维的，它都会被连续地被存储在显存中。

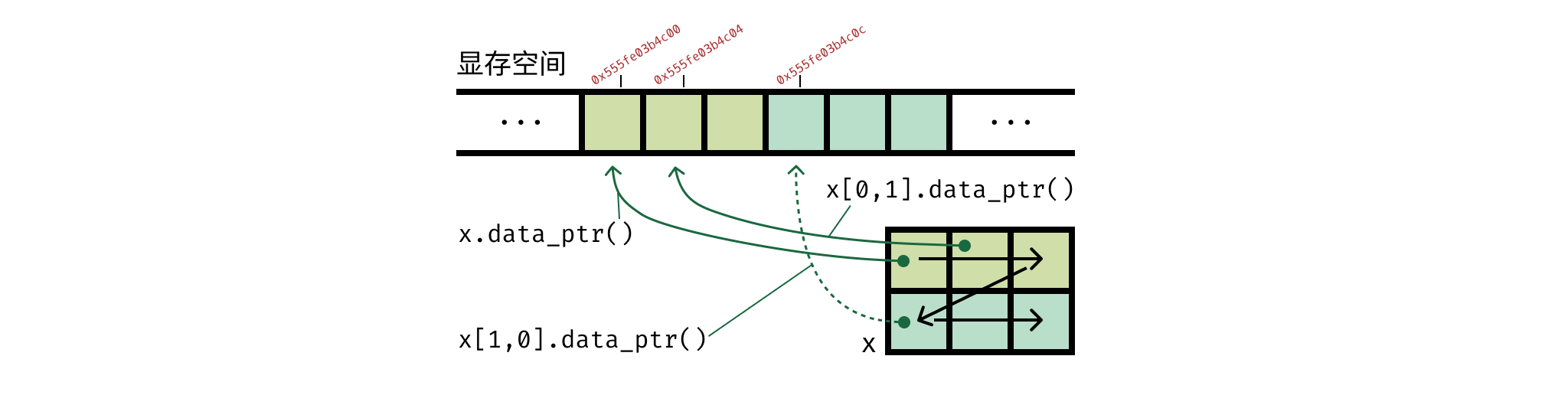
当我们使用 x = torch.empty((2, 3)) 新建一个 Tensor 时，如上图所示，这个新建的矩阵会在内存中申请一块连续的空间，然后按照行优先(也即，先排右侧维度)的顺序，将元素依次存储在显存中。

Sizes 和 Strides

Size 相信大家都比较熟悉，它表示 Tensor 的形状。 Stride 这个词在英文中有步伐的意思，它定义了在每一维度，当前维度的索引加一后 (例如 x[0, 0] -> x[1, 0]) 对应的元素在显存中的地址需要相应地向前移动多少步。

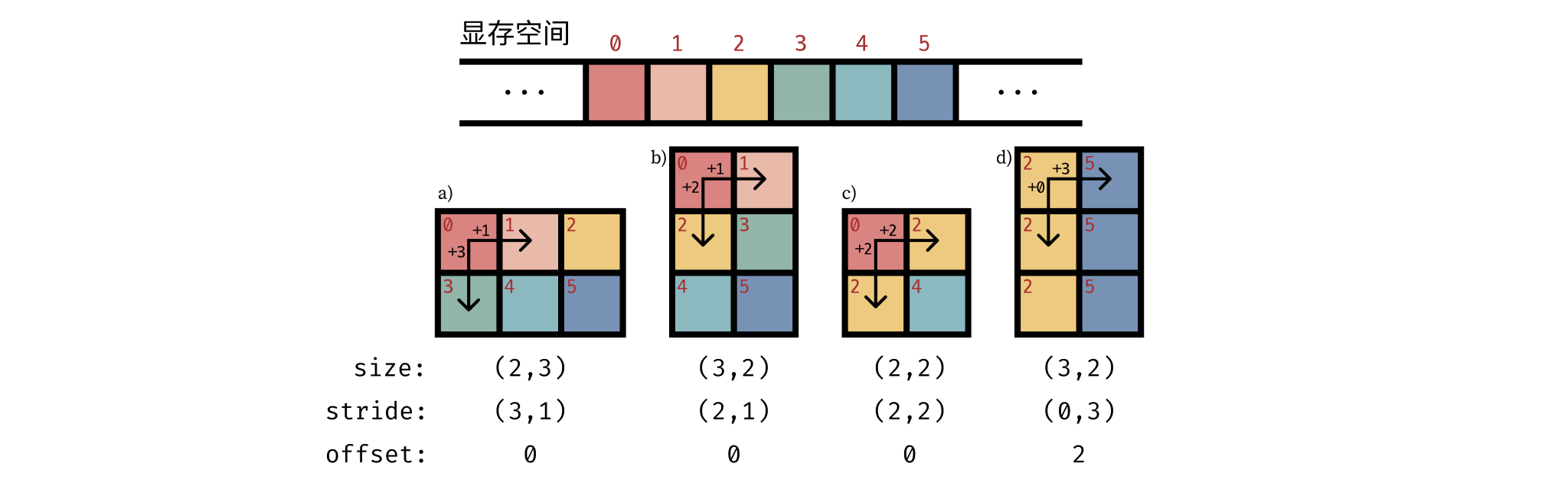
上图中给出了几种不同 size 和 stride 所描述的 Tensor。

一个矩阵按照行优先的顺序读取时，若显存地址是连续的，那么我们就认为该矩阵是连续的 (contiguous)。即该矩阵是按照一个约定俗成的顺序连续地存储在显存中的。例如上图中的 a) 和 b) 都是连续的，而 c) 和 d) 则不是连续的。

注意: 传入 kernel 的 Tensor 我们需要确保它是连续的。否则在 kernel 内读取时，可能会出现意想不到的错误。后续的注意事项中会介绍如何确保 Tensor 是连续的方法。

下面我们简单介绍如何通过设置 stride 来实现一些常见的功能。

View

在利用 view 时，我们的目的是将 Tensor 转为目标形状。假设我们希望目标 Tensor 的形状为 $(D_n, D_{n-1}, \cdots, D_1)$。这时候我们只需要将 stride 设置为 $(\prod_{i=1}^{n-1} D_i, \prod_{i=1}^{n-2} D_i, \cdots, D_1, 1)$ 即可。例如，对于一个维度为 $(2, 3, 4)$ 的张量 stride 应该设置为 $(3 \times 4, 4, 1)$。

import torch

m = 2
n = 3
x = torch.arange(m * n).view(m, n)
print(x)

print(x.view(m, n))
print(
    x.as_strided(
        size=(m, n),
        stride=(n, 1),
    )
)

k = 4
x = torch.arange(m * n * k).view(m, n, k)
print(x.view(m, n, k))
print(
    x.as_strided(
        size=(m, n, k),
        stride=(n * k, k, 1),
    )
)

Expand

在深度学习中，我们经常需要扩展某个维度并重复该维度上的元素形成新的形状。例如，对于一个维度为 $(2, 3, 4)$ 的张量 x，我们希望将其扩展为 $(10, 2, 3, 4)$。即我们希望新的矩阵 y 中 y[0], y[1], … , y[9] 都等于 x。这一操作就可以通过将第 0 维度上的 stride 设置为 0 来实现。

下面是一个简单的维度扩展例子:

import torch

m = 3
n = 4
k = 10
x = torch.arange(m * n).view(m, n)
print(x)

print(x[..., None].expand(m, n, k))
print(
    x.as_strided(
        size=(m, n, k),
        stride=(n, 1, 0),
    )
)

Transpose

转置，也就是交换行列，是一个非常常见的操作，通过修改 stride 可以很方便地实现。如果我们需要将一个矩阵转置，我们只需要交换我们需要 transposed 的两个维度所对应的 stride 即可。

import torch

m = 3
n = 4
x = torch.arange(m * n).view(m, n)
print(x)

print(x.T)
print(
    x.as_strided(
        size=(n, m),
        stride=(1, m),
    )
)

Diagonal

最后一个例子展示如何通过设置 stride 来获取矩阵的对角元素。对于在 $n \times n$ 矩阵中的一个对角元素 $(i, i)$，它的下一个元素应该在 $(i + 1, i + 1)$ 的位置。即在矩阵中下移一步 ($+n$) 后再右移一步 ($+1$)。因此我们只需要将 stride 设置为 $(n + 1,)$ 即可。

import torch

n = 4
x = torch.arange(n * n).view(n, n)
print(x)

print(x.diagonal())
print(
    x.as_strided(
        size=(n,),
        stride=(n + 1,),
    )
)

Triton 中的读与写

在 triton.language 中提供了 load 和 store 两个函数，用于从显存中读取和写入数据。

最为基础的用法是读取或写入指针指向的元素。

x = tl.load(x_ptr)     # 读取指针指向的元素
tl.store(x_ptr, value) # 写入指针指向的元素

需要注意的是，与我们平常写 Python 代码不一样，我们并不是使用 return 来返回结果，而是使用 tl.store 来将结果写入到结果指针指向的元素。 这个结果指针也应该是我们在调用 Kernel 时传入的参数之一。下面是一个简单的例子，它将一个 Tensor x 复制到另一个 Tensor y 中：

import triton.language as tl # 简单起见我们利用 `tl` 来指代 `triton.language` 模块
import triton
import torch

@triton.jit
def copy_kernel(
    x_ptr,
    y_ptr
):
    pid = tl.program_id(0)
    value = tl.load(x_ptr + pid)
    tl.store(y_ptr + pid, value)

if __name__ == "__main__":
    n = 10
    x = torch.randn(n).to("cuda")      # 在 GPU 上分配内存
    y = torch.empty(n).to("cuda")
    copy_kernel[(n, )](x, y)           # y = x.clone()
    print(x)
    print(y)
    print(x.clone())

这里的 y 实际上是操作的输出，但是我们需要在执行 Kernel 之前为它分配空间（在 GPU 上），并作为参数传递给 Kernel。

批量读写

然而在大部分情况下，我们并不仅仅希望只对单个元素进行操作，而是希望像在 Pytorch 中那样对一个 Tensor 进行操作。

下面将介绍三种在 Triton 中通过指针来访问 Tensor 的方法。

多维指针

第一种方式是通过多维指针的形式来描述 Tensor 的形状。简单来说我们算出 Tensor 中每个元素的地址，组成一个地址矩阵，然后通过这个地址矩阵来访问 Tensor 中的元素。值得注意的是，为了正确还原 Tensor 的形状，我们需要将 Tensor 的形状信息传递给 Kernel，例如在下面例子中，我们通过 N 和 M 来传递一个形状为 $(N, M)$ 的 Tensor 的形状信息。

@triton.jit
def plus_one_kernel(
        x_ptr,
        N: tl.constexpr,
        M: tl.constexpr,
        BLOCK_N: tl.constexpr,
        BLOCK_M: tl.constexpr,
    ):
    n_id = tl.program_id(0)
    m_id = tl.program_id(1)

    row_offset = tl.arange(0, BLOCK_N) + n_id * BLOCK_N
    col_offset = tl.arange(0, BLOCK_M) + m_id * BLOCK_M

    index = row_offset[:, None] * M + col_offset[None, :]
    block_ptr = x_ptr + index
    mask = (row_offset[:, None] < N) & (col_offset[None, :] < M)

    x = tl.load(block_ptr, mask=mask) # 读取 mask 为 True 的元素
    tl.store(block_ptr, x + 1, mask=mask) # 写入 mask 为 True 的元素

此外在这个代码中，我们还额外传递了 BLOCK_N 和 BLOCK_M 两个参数。这是因为我们在代码使用了 tl.arange 这一创建 Tensor 的函数。而在 Triton 中，所有的创建 Tensor 的函数都需要 确保每一维度的大小都是 2 的幂。为了避免 N 和 M 不是 2 的幂而出现错误，我们需要利用 triton.next_power_of_2 来对 N 和 M 进行向上取整。此外在 N 和 M 太大的时候，我们可以通过设置一个较小的 BLOCK_N 和 BLOCK_M 将大 Tensor 分为多个小矩阵并行处理。

BLOCK_N = triton.next_power_of_2(N)
BLOCK_M = triton.next_power_of_2(M)

由于 BLOCK_N 和 BLOCK_M 和 N 与 M 的值可能不一致，在计算 offset 时，我们需要利用引入一个掩码 musk 来确保我们只读写 N 和 M 范围内的元素。

上图是我们加载 $(2, 3)$ 矩阵的示意图。由于 BLOCK_M 需要设置为 $2$ 的幂 ($4$), 因此在计算 offset 时，每一行的末尾会多出 $1$ 个元素。我们需要通过 mask 来确保屏蔽掉这些多出的元素。

块指针 (Block Pointer)

我们可以看到上面一种方法写起来是非常麻烦的。第二种方式是利用块指针 (Block Pointer) 来描述 Tensor 的形状。它为我们提供了更简洁的写法，我们不再需要手动地构建指针矩阵和手动设置 mask。

@triton.jit
def plus_one_kernel(
        x_ptr,
        N: tl.constexpr,
        M: tl.constexpr,
        BLOCK_N: tl.constexpr,
        BLOCK_M: tl.constexpr,
    ):
    n_id = tl.program_id(0)
    m_id = tl.program_id(1)

    block_ptr = tl.make_block_ptr(
        x_ptr, # 父 Tensor 的指针，指向第一个元素
        shape=(N, M), # 描述父 Tensor 的形状
        strides=(M, 1), # 描述父 Tensor 的 strides
        offsets=(n_id * BLOCK_N, m_id * BLOCK_M), # 描述每个维度上的偏移量
        block_shape=(BLOCK_N, BLOCK_M), # 描述块的大小
        order=(1, 0) # 描述在原始 Tensor 中每一维度的顺序。例如如果 strides 为 (1, M), 既转置后的 `x`，这时候 order 应该设置为 (0, 1)
    )

    x = tl.load(block_ptr, boundary_check=(0, 1))
    tl.store(block_ptr, x + 1, boundary_check=(0, 1))

张量描述符 (Tensor Descriptor)

最后一种方法是利用张量描述符 (Tensor Descriptor) 来描述 Tensor 的形状并进行加载。从用法来看它和块指针非常相似，但是它利用了 TMA 技术来进一步压榨 GPU 的性能。

该方法在 3.3.0 版本中作为实验 API (_experimental_make_tensor_descriptor) 被加入，并在 3.4.0 中成为正式 API (make_tensor_descriptor) 值得注意的是，只有在 Hopper 之后的 GPU，即 H 系列和 B 系列以后的 GPU，才支持 TMA 技术。

@triton.jit
def plus_one_kernel(
        x_ptr,
        N: tl.constexpr,
        M: tl.constexpr,
        BLOCK_N: tl.constexpr,
        BLOCK_M: tl.constexpr,
    ):
    n_id = tl.program_id(0)
    m_id = tl.program_id(1)

    tensor_desc = tl.make_tensor_descriptor(
        x_ptr, # Tensor 的指针，指向第一个元素
        shape=(N, M), # Tensor 的形状
        strides=(M, 1), # Tensor 的 strides
        block_shape=(BLOCK_N, BLOCK_M) # 要处理的块的大小
    )

    x = tensor_desc.load(n_id * BLOCK_N, m_id * BLOCK_M) # 根据 offset 读取指定的块
    tensor_desc.store(n_id * BLOCK_N, m_id * BLOCK_M, x + 1)

注意事项

在 Triton 中进行读写操作时，我们需要注意以下两点 输入 Tensor 是否连续 和 边界检查。

注意输入 Tensor 是否连续

如前文所描述的，传入 Kernel 的 Tensor 是一个指针。若我们希望在 Kernel 中以 Tensor 的形式访问数据，我们需要利用 shape 和 stride 等形象来重构 Tensor。在重构的时候，为了方便起见，我们一般约定 Tensor 是按照行优先的顺序存储的。即，这个 Tensor 是连续的 (contiguous)。

然而，如前文中所提到的，有些操作会改变 Tensor 的连续性。因此我们在将 Tensor 传入 Kernel 之前，需要确保 Tensor 是连续的。

if not tensor.is_contiguous():
    tensor = tensor.contiguous()

事实上手动检查输入 Tensor 是否连续是十分烦人的，也很容易忘记。这时候使用装饰器来确保输入 Tensor 是连续的会是一个很好的选择。这里十分推荐参考 Flash-linear-attention 中的 input_guard 装饰器。

def input_guard(
    fn: Callable[..., torch.Tensor]
) -> Callable[..., torch.Tensor]:
    """
    A decorator to make sure all input tensors are contiguous and set the device based on input tensors.
    """

    @functools.wraps(fn)
    def wrapper(*args, **kwargs):
        contiguous_args = (i if not isinstance(i, torch.Tensor) else i.contiguous() for i in args)
        contiguous_kwargs = {k: (v if not isinstance(v, torch.Tensor) else v.contiguous()) for k, v in kwargs.items()}

        tensor = None
        for arg in args:
            if isinstance(arg, torch.Tensor):
                tensor = arg
                break
        if tensor is None:
            for value in kwargs.values():
                if isinstance(value, torch.Tensor):
                    tensor = value
                    break

        if tensor is not None:
            ctx = custom_device_ctx(tensor.device.index)
        else:
            ctx = contextlib.nullcontext()

        with ctx:
            return fn(*contiguous_args, **contiguous_kwargs)

    return wrapper

边界检查

在 Kernel 中，我们可以通过指针访问到整个显存空间。如果不多加小心，例如没有检查边界时，计算错误的偏移量，可能会导致 Kernel 访问到不属于它的数据，甚至修改其他数据。因此在读写，尤其是写的时候，需要格外注意检查边界。

不进行边界检查会如何？ 为了探讨这一问题我们看下面的代码。下面的代码实现一个非常简单的功能：为矩阵中第 offset 个元素赋值。

import triton.language as tl
import triton
import torch

@triton.jit
def set_value_kernel(x_ptr, offset, value):
    # 将 offset 对应的元素设置为 value
    tl.store(x_ptr + offset, value)

if __name__ == "__main__":
    # 初始化
    x = torch.zeros((2, 3)).to("cuda")
    a, b = x
    print(f"a.shape: {a.shape}; b.shape: {b.shape}")
    print(f"a: {a}; b: {b}\n")

    print("对 a 进行越界赋值")
    try:
        a[3] = 1.0
    except Exception as e:
        print(e)
    print(f"a: {a}; b: {b}\n")

    print("使用 triton 对 a 进行越界赋值")
    set_value_kernel[(1,)](a, 3, 1.0)
    print(f"a: {a}; b: {b}\n")

运行上面代码，我们会得到如下输出：

a.shape: torch.Size([3]); b.shape: torch.Size([3])
a: tensor([0., 0., 0.], device='cuda:0'); b: tensor([0., 0., 0.], device='cuda:0')

对 a 进行越界赋值
index 3 is out of bounds for dimension 0 with size 3
a: tensor([0., 0., 0.], device='cuda:0'); b: tensor([0., 0., 0.], device='cuda:0')

使用 triton 对 a 进行越界赋值
a: tensor([0., 0., 0.], device='cuda:0'); b: tensor([1., 0., 0.], device='cuda:0')

我们可以看到，尽管我们只向 set_value_kernel 传递了 Tensor a 的指针，但是最终 b 也被修改了。

因此，在 Triton 中，我们在进行读写操作时需要格外注意，避免意外修改其他数据。

如何避免越界？

若使用多维指针的方式来进行读写，我们可以设置 mask，在 mask 中将需要读写的元素设置为 True，其余元素设置为 False，即可避免越界访问。在默认情况下，padding 位置的元素会被设置为 $0$。但是也可通过 other 参数来设置 padding 元素的值。
若使用块指针的方式来进行读写，我们可以设置 boundary_check 参数来指定对哪些维度进行边界检查。在默认情况下，会使用 $0$ 来填充边界外的元素。