词法标记中的HMM和CRF
前言
第一次与HMM和CRF的接触,体验不是很好。公式中每个符号的意思都懂,但和在一起后就完全看不懂,于是虽然程序是编出来了,但是对于模型是完全没有一点理解,出了问题也是在盲目地trial and error。22号到今天,我尝试着将HMM和CRF中一些常用的公式,如向前、向后算法,推了一遍,并试图理解推导过程中产生的语义。
隐马尔可夫模型
定义
隐马尔可夫模型是关于时态的概率模型,描述有一个隐藏的马尔可夫链随机生成不可观测的状态随机序列,再由各个状态生成一个观测状态的过程。1
首先什么是马尔可夫链?马尔可夫链就是一个状态机,状态机由当前状态 $Y_t$ 根据给定概率 $\mathcal{T}$ 随机地转移到下一个状态 $Y_{t+1}$,从而产生一条态随机序列。
下面给出一个包含5个状态 $Y \in \lbrace y_1,y_2,y_3,y_4,y_5\rbrace$ 的状态机,其中 $\mathcal{T}(y_4 \to y_5)$ 表示马尔可夫链中由状态 $y_4$ 转移到状态 $y_5$ 的概率

下面是该马尔可夫链可能生成的一条状态随机序列

在隐马尔可夫模型中,我们假设由马尔可夫链生成的隐藏状态我们是无法直接观测到的,我们只能够观察到由这些隐藏状态随机生成的观测量。
在日常生活中我们也能够找到这样的例子,我们用水壶煮水,水的温度我们往往是无法观测的(在这里我们使用的水壶,是最简单的那种纯粹的不锈钢水壶没有任何的附加功能),但是有些状态我们是可以观察到的,比如:水壶发出的声响、壶口冒出的水汽。通过隐马尔可夫模型我们对水温随着时间的变化和水温和声响之间进行建模,我们就可以通过发出的响声来估算水温。另外,在某些领域,就算状态量可以被直接测量,但是因为仪器原因,或者由于线路干扰,最终测量人员看到的数值和原始数值会存在出入,通过隐马尔可夫模型我们也能在一定程度上消除这样的误差或干扰。
在词性标注任务中,我们可以将词性作为无法被直接观测到的隐藏状态,而将词语作为观测值。下面我们都以词性标注为例子讲解隐马尔可夫模型中的三个问题。
三个基本问题
隐马尔可夫模型有三个基本问题:概率计算问题、预测问题和学习问题。
为了方便计算,我对隐马尔可夫模型进行一些拓展,其中 $\text{Start}$ 表示开始状态,$\text{Stop}$ 表示结束状态,隐藏状态 $\lbrace Y_1,\dotsc,Y_n\rbrace$ 为词性标注,观测状态 $\lbrace S_1,\dotsc,S_n\rbrace$ 为句子 $S$ 位于位置 $i$ 的词语,我们规定 $P(\text{Start}) = P(\text{Stop}) = 1$

概率计算问题
概率计算问题是给定句子 $S=(s_1,s_2,\dotsc,s_n)$ 计算 $P(S)$,其实这在词性标注中用得不多, 但是会出现在使用隐马尔可夫模型解决其他问题中。
根据概率图模型,我们可很容易地求出整个模型的联合分布,而 $P(S)$ 就是在这个联合分布上求边缘分布了
其中
\[P(S_1,\dotsc,S_n,Y_1,\dotsc,Y_n) = P(Y_1|\text{Start})P(S_1|Y_1) \dotsm P(Y_n|Y_{n-1})P(S_n|Y_n)P(\text{Stop}|Y_n)\]我们使用和-积变量消除可以将 $\sum_{Y_1,\dotsc,Y_n}$ 分解到乘积中如
\[\begin{split} P(S) &= \sum_{Y_1,\dotsc,Y_n}{P(S_1,\dotsc,S_n,Y_1,\dotsc,Y_n)}\\ &= \sum_{Y_n}P(\text{Stop}|Y_n)P(S_n|Y_n)\dotsm\sum_{Y_2}P(Y_3|Y_2)P(S_2|Y_2)\sum_{Y_1}P(Y_2|Y_1)P(S_1|Y_1)P(Y_1|\text{Start}) \end{split}\]我们可以看到最底层的 $\sum_{Y_1}P(S_1|Y_1)P(Y_1|\text{Start})$ 会被重复计算,因此我们可以将它的值用 $\alpha$ 存储起来,而避免重复计算,这就是动态规划的思想。
于是我们有
-
初始值
\[\begin{split} \alpha_1 &= P(Y_1|\text{Start})P(S_1|Y_1)\\ &= P(\text{Start})P(Y_1|\text{Start})P(S_1|Y_1)\\ &= P(Y_1)P(S_1|Y_1)\\ &= P(S_1, Y_1) \end{split}\] -
递推 对 $i = 2,3,\dotsc,n$
\[\begin{split} \alpha_i &= P(S_i|Y_i)\sum_{Y_{i-1}}\left(P(Y_i|Y_{i-1})\alpha_{i-1}\right)\\ &= P(S_i|Y_i)\sum_{Y_{i-1}}\left(P(Y_i|Y_{i-1})P(S_1,\dotsc, S_{i-1}, Y_{i-1})\right)\\ &= P(S_i|Y_i)\sum_{Y_{i-1}}P(S_1,\dotsc, S_{i-1}, Y_i, Y_{i-1})\\ &= P(S_i|Y_i)P(S_1,\dotsc, S_{i-1}, Y_i)\\ &= P(S_1,\dotsc, S_i, Y_i) \end{split}\] -
结束
\[\begin{split} P(S) &= \sum_{Y_n}\left(P(\text{Stop}|Y_n)\alpha_{n}\right)\\ &= \sum_{Y_n}P(S_1,\dotsc, S_n, Y_i) &= P(S_1,\dotsc, S_n) \end{split}\]
从上面三个过程中我们可以很清楚地看到 $\alpha_i$ 所代表的含义是什么:位置 $i$ 的标记 $Y_i$ 与从开始到 $i$ 的词语 ${S_1,S_2,\dotsc,S_i}$ 的联合概率
\[P(S_1,\dotsc, S_i, Y_i)\]上述过程称为向前算法,和-积变量消除与随机变量直接的顺序无关因此 $P(S)$ 使用和-积变量消除还能 $\sum_{Y_1,\dotsc,Y_n}$ 分解成如下形式
\[\begin{split} P(S) &= \sum_{Y_1,\dotsc,Y_n}{P(S_1,\dotsc,S_n,Y_1,\dotsc,Y_n)}\\ &= \sum_{Y_1}P(Y_1|\text{Start})P(S_1|Y_1)\sum_{Y_2}P(Y_1|Y_2)P(S_2|Y_2) \dotsm \sum_{Y_n}P(Y_n|Y_{n-1})P(S_n|Y_n)P(\text{Stop}|Y_n) \end{split}\]对这个公式我们有
-
初始值
\[\beta_n = P(\text{Stop}|Y_n)\] -
递推 对 $i = n-1,n-2,\dotsc,1$
\[\begin{split} \beta_i &= \sum_{Y_{i+1}}\left(P(Y_{i+1}|Y_i)P(S_{i+1}|Y_{i+1})\beta_{i+1}\right)\\ &= \sum_{Y_{i+1}}\left(P(Y_{i+1}|Y_i)P(S_{i+1}|Y_{i+1})P(S_{i+2},\dotsc,S_n|Y_{i+1})\right)\\ &= \sum_{Y_{i+1}}\left(\frac{1}{P(Y_i)}P(Y_i|Y_{i+1})P(S_{i+1}|Y_{i+1})P(S_{i+2},\dotsc,S_n, Y_{i+1})\right)\\ &= \sum_{Y_{i+1}}\left(\frac{1}{P(Y_i)}P(Y_i|Y_{i+1})P(S_{i+1},\dotsc,S_n, Y_{i+1})\right)\\ &= \sum_{Y_{i+1}}\left(\frac{1}{P(Y_i)}P(S_{i+1},\dotsc,S_n, Y_i, Y_{i+1})\right)\\ &= \sum_{Y_{i+1}}P(S_{i+1},\dotsc,S_n, Y_{i+1}|Y_i)\\ &= P(S_{i+1},\dotsc,S_n|Y_i) \end{split}\] -
结束
\[\begin{split} P(S) &= \sum_{Y_1}\left(P(Y_1|\text{Start})P(S_1|Y_1)\beta_1\right)\\ &= \sum_{Y_1}P(S_1,\dotsc,S_n|Y_1) &= P(S_1,\dotsc, S_n) \end{split}\]
其中 $\beta_i$ 表达的物理内涵为:从 $i+1$ 到结束的词语 ${S_1,S_2,\dotsc,S_i}$ 在给定位置 $i$ 的标记 $Y_i$ 的情况下的联合条件概率
\[P(S_{i+1},\dotsc,S_n|Y_i)\]值得我们注意的是,向前和向后算法的中间变量所表达的物理含义是不同的,$\alpha$ 表达的是一个联合分布,而 $\beta$ 则表示了一个条件分布
\[\begin{split} \beta_i &= P(S_{i+1},\dotsc,S_n|Y_i) \\ \alpha_i &= P(S_1,\dotsc, S_i, Y_i) \end{split}\]在隐马尔可夫模型中有一个很好的性质,方便我们的计算,那就是给定 $Y_j$ 的条件下会阻断所有途径 $Y_j$ 的概率影响,即存在着很多有关 $Y_j$ 的条件独立

因为存在 $S_i$ 与 $\mathbf S_{-i}$在给定 $Y_i$ 的条件下独立,即 $(S_i\bot \mathbf S_{-i} |Y_i)$,其中 $S_{-i}$ 代表模型 $S$ 中除位置 $i$ 外的其他观察变量的集合,我们有如下公式
\[\begin{split} &P(S_i|Y_i)P(\mathbf{S}_{-i}, Y_i)\\ = &P(S_i|Y_i)P(\mathbf{S}_{-i}|Y_i)P(Y_i)\\ = &P(\mathbf{S}_{-i}, S_i|Y_i)P(Y_i)\\ = &P(\mathbf{S}_{-i}, S_i, Y_i)\\ \end{split}\]同理对任意 $i < j < k$ 有 任意 $Y_i$ 在给定 $Y_j$ 的条件下与 $S_j$ 和 $S_k$ 独立,即 $(S_k, S_j\bot Y_i |Y_j)$ ,对应的也有 $(S_i, S_j\bot Y_k |Y_j)$,所以我们有公式
\[\begin{equation} \begin{split} &P(Y_i|Y_j)P(S_k, S_{k+1}, \dotsc, S_n, Y_j)\\ = &P(Y_i|Y_j)P(S_k, S_{k+1}, \dotsc, S_n|Y_j)P(Y_j)\\ = &P(S_k, S_{k+1}, \dotsc, S_n, Y_i|Y_j)P(Y_j)\\ = &P(S_k, S_{k+1}, \dotsc, S_n, Y_i, Y_j)\\ \end{split} \end{equation}\] \[\begin{equation} \begin{split} &P(Y_k|Y_j)P(S_1, S_i, \dotsc, S_k, Y_j)\\ = &P(Y_k|Y_j)P(S_1, S_i, \dotsc, S_k|Y_j)P(Y_j)\\ = &P(S_1, S_i, \dotsc, S_k, Y_i|Y_j)P(Y_j)\\ = &P(S_1, S_i, \dotsc, S_k, Y_i, Y_j)\\ \end{split} \end{equation}\]预测问题
预测问题也叫做解码问题,实际上是一个最大后验查询,即给定条件变量,查询其他变量的最有可能取值
在词性标注任务中,这就表现为,给定一个句子 $S$ 寻找最有可能的标记序列 $Y^\star$
在计算 $\mathop{\text{argmax}}_{Y}P(Y,S)$ 的时候我们同样也能使用最大-积变量消除
\[\begin{split} \mathop{\text{argmax}}_{Y}P(Y,S) &= \mathop{\text{argmax}}_{Y_1,\dotsc,Y_n}{P(Y_1,\dotsc,Y_n,S)}\\ &= \mathop{\text{argmax}}_{Y_n}P(\text{Stop}|Y_n)P(S_n|Y_n)\dotsm\mathop{\text{argmax}}_{Y_2}P(Y_3|Y_2)P(S_2|Y_2)\mathop{\text{argmax}}_{Y_1}P(Y_2|Y_1)P(S_1|Y_1)P(Y_1|\text{Start}) \end{split}\]注:max是求最大值,argmax是最大值时自变量的取值
同样地我们可以使用动态规划来减少重复的计算,这个算法又叫做维比特算法
-
初始值
\[\delta_1 = P(Y_1|\text{Start})P(S_1|Y_1)\\ \varPsi_1 = 0\] -
递推 对 $i = 2,3,\dotsc,n$
\[\delta_i = P(S_i|Y_i)\max_{Y_{i-1}}\left(P(Y_i|Y_{i-1})\cdot\delta_{i-1}\right) \\ \begin{split} \varPsi_i &= P(S_i|Y_i)\mathop{\text{argmax}}_{Y_{i-1}}\left(P(Y_i|Y_{i-1})\cdot\delta_{i-1}\right)\\ &= \mathop{\text{argmax}}_{Y_{i-1}}\left(P(Y_i|Y_{i-1})\cdot\delta_{i-1}\right) \end{split}\] -
结束
\[\max_{Y}P(Y|S) = \max_{Y_n}\delta_{n}\\ Y_n^\star=\mathop{\text{argmax}}_{Y_n}\delta_{n}\] -
最优路径回溯 对 $i = n-1,n-2,\dotsc,1$
\[Y_i^\star=\varPsi_{i+1}(Y_{i+1}^*)\]
对此我们可以得到最优的词性标注序列 $Y^\star={Y_1^\star,Y_2^\star,\dotsc,Y_n^\star}$
学习问题
有向图模型的学习十分简单。我们利用极大似然估计就可以完成学习,也就是说,我们只需要在训练集中统计得出,转移概率 $P(Y_i|Y_{i-1})$ 和发射概率 $P(S_i|Y_i)$ 即可。
条件随机场
定义
条件随机场是给定随机变量 $S$ 条件下,随机变量 $Y$ 的马尔可夫随机场。1
其实我觉得条件随机场与马尔可夫网模型,在结构上没有什么太大的区别,只不过最终马尔可夫随机场使用其联合分布,而条件随机场使用其条件分布罢了
马尔可夫网中的联合分布
\[P(S,Y)=\frac{1}{Z}\prod_{\mathbf{D}}\phi(\mathbf{D})\\ Z=\sum_{S,Y}\prod_{\mathbf{D}}\phi(\mathbf{D})\\\]条件随机场中的条件分布
\[P(Y|S)=\frac{1}{Z(X)}\prod_{\mathbf{D}}\phi(\mathbf{D})\\ Z(X)=\sum_{Y}\prod_{\mathbf{D}}\phi(\mathbf{D})\]我们可以看到这两个分布是可以相互转换的
\[\begin{split} P(Y|S)&=\frac{1}{Z(X)}\prod_{\mathbf{D}}\phi(\mathbf{D})\\ &=\frac{\prod_{\mathbf{D}}\phi(\mathbf{D})}{\sum_{Y}\prod_{\mathbf{D}}\phi(\mathbf{D})}\\ &=\frac{\frac{1}{Z}\prod_{\mathbf{D}}\phi(\mathbf{D})}{\frac{1}{Z}\sum_{Y}\prod_{\mathbf{D}}\phi(\mathbf{D})}\\ &=\frac{P(S,Y)}{P(S)}=\frac{P(S,Y)}{\sum_{Y}P(S,Y)}\\ \end{split}\]在词性标注中我们常用的是线性链条件随机场,在线性链随机场中句子 $S$ 不再像在隐马尔可夫模型那样展开到每一个位置,而是作为一个整体出现,将句子的信息尽可能地保留

线性链条件随机场的分布
由于条件随机场是无向图模型,因此它的分布不能像隐马尔可夫模型那样,计算条件分布的乘积即可。而是需要计算团上的因子的乘积。在线性链条件随机场中,由于模型的形状特别好——图可以被分为许多个以 ${Y_{i-1},Y_i,S}$ 构成的三角形团。因此我们可以将线性链条件随机场中的分布表示为
\[P(Y|S)=\frac{1}{Z(S)}\tilde{P}(Y,S)\\ \tilde{P}(Y,S)=\prod_{i=1}^{n+1}\phi(Y_i,Y_{i-1},S)\\ Z(S)=\sum_Y\tilde{P}(Y,S)\]其中 $\tilde{P}(Y,S)$ 称为未归一化概率,同时 $Y_0=\text{Start}$ 类似的 $Y_{n+1}=\text{Stop}$ ,但我们观察上式,我们还是不能像隐马尔可夫模型中那样清晰地理解因子的具体内涵。于是乎,我们可以更进一步地改造因子,即将其转换到对数空间中去
\[\phi(Y_i,Y_{i-1},S)=\exp(\mathop{\mathcal{Score}}(S,i,Y_{i-1},Y_i))\]其中函数 $\mathop{\mathcal{Score}}(S,i,Y_{i-1},Y_i)$ 是得分函数,可以被写为权重向量 $\boldsymbol{w}$ 与0-1特征向量 $\boldsymbol{f}(S,i,Y_{i-1},Y_i)$ 的点乘,即
\[\mathop{\mathcal{Score}}(S,i,Y_{i-1},Y_i)=\boldsymbol{w}\cdot \boldsymbol{f}(S,i,Y_{i-1},Y_i)\]特征向量 $\boldsymbol{f}$ 在词性标注任务中往往通过如下模板来生成
\[\begin{array}{l} \hline \begin{array}{ll} 01: y_{i} \circ y_{i-1} & 02: y_{i} \circ s_{i}\\ 03: y_{i} \circ s_{i-1} & 04: y_{i} \circ s_{i+1}\\ 05: y_{i} \circ s_{i} \circ c_{i-1,-1} & 06: y_{i} \circ s_{i} \circ c_{i+1,1}\\ 07: y_{i} \circ c_{i,1} & 08: y_{i} \circ c_{i,-1}\\ \end{array}\\ \begin{array}{l} 09: y_{i} \circ c_{i,k} , 1 < k < \#c_{i}\\ 10: y_{i} \circ c_{i,1} \circ c_{i,k}, 1 < k < \#c_{i}\\ 11: y_{i} \circ c_{i,-1} \circ c_{i,k}, 1 < k < \#c_{i}\\ 12: \mathbf{if}\; \#c_{i} = 1 \;\mathbf{then}\; y_{i} \circ w_{i} \circ c_{i-1, -1} \circ c_{t+1,1}\\ 13: \mathbf{if}\; c_{i, k} = c_{i, k+1} \;\mathbf{then}\; y_{i} \circ c_{i,k} \circ \mathit{“Consecutive"}\\ 14: y_{i} \circ \mathsf{prefix}\! \left(w_{i} , k\right) , 1 \leq k \leq 4 , k \leq \#c_{i}\\ 15: y_{i} \circ \mathsf{suffix}\! \left(w_{i} , k\right) , 1 \leq k \leq 4 , k \leq \#c_{i}\\ \end{array}\\ \hline \end{array}\]其中 $\circ$ 代表字符串串联; $s_{i}$ 表示第 $i$ 个位置上的词性标注; $y_i$ 表示位置 $i$ 上的词性标注; $c_{i, k}$ 表示第 $i$ 个词 $s_{i}$ 上第 $k$ 个位置的字符,特别地有 $c_{i, -1}$ 是 $s_{i}$ 上最后一个字符; $\#c_{i}$ 表示 $s_{i}$ 中字符的个数; $\mathsf{prefix}\! \left(w_{i} , k\right)$ 和 $\mathsf{suffix}\! \left(w_{i} , k\right)$ 分别表示着 $s_{i}$ 中长度为 $k$ 的前缀和后缀。
除了使用特征模板来生成特征向量,我们也可以使用神经网络,例如LSTM和GRU等来生成。
三个基本问题
条件随机场同样有三个基本问题:概率计算问题、预测问题和学习问题。
由于在概率计算上与隐马尔可夫模型存在着差异,因此着三个问题的在解法上也存在着不同,其中概率计算问题、预测问题在思路上与隐马尔可夫模型是一致的,但在学习问题上就有着天壤之别了,这主要是因为
造成这种差异的最主要原因或许是马尔可夫网与贝叶斯网之间存在的关键差别——使用全局归一化常数(即配分函数),而不是使用每个CPD中的局部归一化。这种全局化因子使得网络中的所有参数耦合,进而导致无法分解的问题以及无法分别估计局部参数。2
但幸运的时候我们有其他算法可以解决这个问题。
概率计算问题
在条件随机场中有两个我们特别关系的概率 $P(Y_i|S)$ ,即在给定句子 $S$ 时,位置 $i$ 的标记的概率。和 $P(Y_{i-1},Y_i|S)$
\[\begin{split} P(Y_i|S) &= \sum_{Y_{\neq i}}P(Y_1,Y_2,\dotsc,Y_n|S)\\ &= \frac{1}{Z(S)}\sum_{Y_{\neq i}}\tilde{P}(Y_1,Y_2,\dotsc,Y_n,S)\\ &= \frac{1}{Z(S)}\sum_{Y_{\neq i}}\phi(\text{Start},Y_1,S)\phi(Y_1,Y_2,S)\dotsm\phi(Y_n,\text{Stop},S)\\\\ P(Y_{i-1},Y_i|S) &= \sum_{Y_{\neq \{i,i-1\}}}P(Y_1,Y_2,\dotsc,Y_n,S)\\ &= \frac{1}{Z(S)}\sum_{Y_{\neq \{i,i-1\}}}\tilde{P}(Y_1,Y_2,\dotsc,Y_n,S)\\ &= \frac{1}{Z(S)}\sum_{Y_{\neq \{i,i-1\}}}\phi(\text{Start},Y_1,S)\phi(Y_1,Y_2,S)\dotsm\phi(Y_n,\text{Stop},S)\\\\ Z(S) &= \sum_{Y_1,Y_2,\dotsc,Y_n}\tilde{P}(Y_1,Y_2,\dotsc,Y_n,S)\\ &= \sum_{Y_1,Y_2,\dotsc,Y_n}\phi(\text{Start},Y_1,S)\phi(Y_1,Y_2,S)\dotsm\phi(Y_n,\text{Stop},S)\\ \end{split}\]对未归一化概率 $\tilde{P}(Y_1,Y_2,\dotsc,Y_n,S)$ 的求和进行了多次,并且有着共同点
\[\begin{split} &\sum_{Y_{\neq i}}\tilde{P}(Y_1,Y_2,\dotsc,Y_n,S)\\ =&\sum_{Y_{\neq i}}\phi(\text{Start},Y_1,S)\phi(Y_1,Y_2,S)\dotsm\phi(Y_n,\text{Stop},S)\\ =&\sum_{Y_1,\dotsc,Y_{i-1}}\phi(\text{Start},Y_1,S)\dotsm\phi(Y_{i-1},Y_i,S)\sum_{Y_{i+1},\dotsc,Y_n}\phi(Y_i,Y_i+1,S)\dotsm\phi(Y_n,\text{Stop},S)\\ \\ &\sum_{Y_{\neq \{i,i-1\}}}\tilde{P}(Y_1,Y_2,\dotsc,Y_n,S)\\ =&\sum_{Y_{\neq \{i,i-1\}}}\phi(\text{Start},Y_1,S)\phi(Y_1,Y_2,S)\dotsm\phi(Y_n,\text{Stop},S)\\ =&\sum_{Y_1,\dotsc,Y_{i-2}}\phi(\text{Start},Y_1,S)\dotsm\phi(Y_{i-2},Y_{i-1},S)\cdot\phi(Y_{i-1},Y_i,S)\cdot\sum_{Y_{i+1},\dotsc,Y_n}\phi(Y_i,Y_i+1,S)\dotsm\phi(Y_n,\text{Stop},S)\\ \\ &\sum_{Y_1,Y_2,\dotsc,Y_n}\tilde{P}(Y_1,Y_2,\dotsc,Y_n,S)\\ =&\sum_{Y_1,Y_2,\dotsc,Y_n}\phi(\text{Start},Y_1,S)\phi(Y_1,Y_2,S)\dotsm\phi(Y_n,\text{Stop},S)\\ =&\sum_{Y_1}\phi(\text{Start},Y_1,S)\dotsm\sum_{Y_i}\phi(Y_{i-1},Y_i,S)\sum_{Y_{i+1},\dotsc,Y_n}\phi(Y_i,Y_i+1,S)\dotsm\phi(Y_n,\text{Stop},S)\\ =&\sum_{Y_n}\phi(Y_n,\text{Stop},S)\dotsm\sum_{Y_i}\phi(Y_i,Y_{i+1},S)\sum_{Y_1,\dotsc,Y_{i-1}}\phi(\text{Start},Y_1,S)\dotsm\phi(Y_{i-1},Y_i,S)\\ =&\sum_{Y_1,\dotsc,Y_i}\phi(\text{Start},Y_1,S)\dotsm\phi(Y_{i-1},Y_i,S)\sum_{Y_{i+1},\dotsc,Y_n}\phi(Y_i,Y_i+1,S)\dotsm\phi(Y_n,\text{Stop},S)\\ \end{split}\]我们可以看到这三个问题都可以使用和-积变量消除分解为
- 向前求和 $\sum_{Y_1,\dotsc,Y_{i-1}}\phi(\text{Start},Y_1,S)\dotsm\phi(Y_{i-1},Y_i,S)$
- 向后求和 $\sum_{Y_{i+1},\dotsc,Y_n}\phi(Y_i,Y_i+1,S)\dotsm\phi(Y_n,\text{Stop},S)$
这两部分。
于是我们就得到了条件随机场中的向前-向后算法
-
初始值
\[\begin{split} \alpha_0 &= \phi(\text{Start},Y_1,S)\\\\ \beta_{n+1} &= \phi(Y_n,\text{Stop},S)\\ \end{split}\] -
递推 对 $i = 2,3,\dotsc,n$
\[\begin{split} \alpha_i &= \sum_{Y_{i-1}}\left(\phi(Y_{i-1},Y_i,S)\alpha_{i-1}\right)\\\\ \beta_i &= \sum_{Y_{i+1}}\left(\phi(Y_i,Y_{i+1},S)\beta_{i+1}\right)\\ \end{split}\] -
结束
最后我们有
\[\begin{split} \alpha_i &= \sum_{Y_1,\dotsc,Y_{i-1}}\phi(\text{Start},Y_1,S)\dotsm\phi(Y_{i-1},Y_i,S)\\\\ \beta_i &= \sum_{Y_{i+1},\dotsc,Y_n}\phi(Y_i,Y_i+1,S)\dotsm\phi(Y_n,\text{Stop},S)\\ \end{split}\]于是我们可以利用 $\alpha$ 和 $\beta$ 很快地将 $P(Y_i|S)$ 、 $P(Y_{i-1},Y_i|S)$ 以及 $Z(S)$ 快速地求出
\[\begin{split} P(Y_i|S) &= \alpha_i\beta_i\\\\ P(Y_{i-1},Y_i|S) &= \alpha_{i-1}\phi(Y_{i-1},Y_i,S)\beta_i\\\\ Z(S) &= \sum_{Y_n}\alpha_n\\ &= \sum_{Y_1}\beta_1\\ &= \sum_{Y_i}\left(\alpha_i\beta_i\right) \end{split}\]
现在我们需要思考一个问题, $\alpha_i$ 与 $\beta_i$ 所代表的物理内涵是什么?观察他们的式子我们可以说
- $\alpha_i$ 表示在位置 $i$ 的标记是 $Y_i$ 并且到位置 $i$ 的前部分标记序列的非规范化概率;
- $\beta_i$ 表示在位置 $i$ 的标记是 $Y_i$ 并且从 $i+1$ 到 $n$ 的后部分标记序列的非规范化概率;1
对于一个条件随机场 $\mathcal{H}$ 我们考虑两个子图
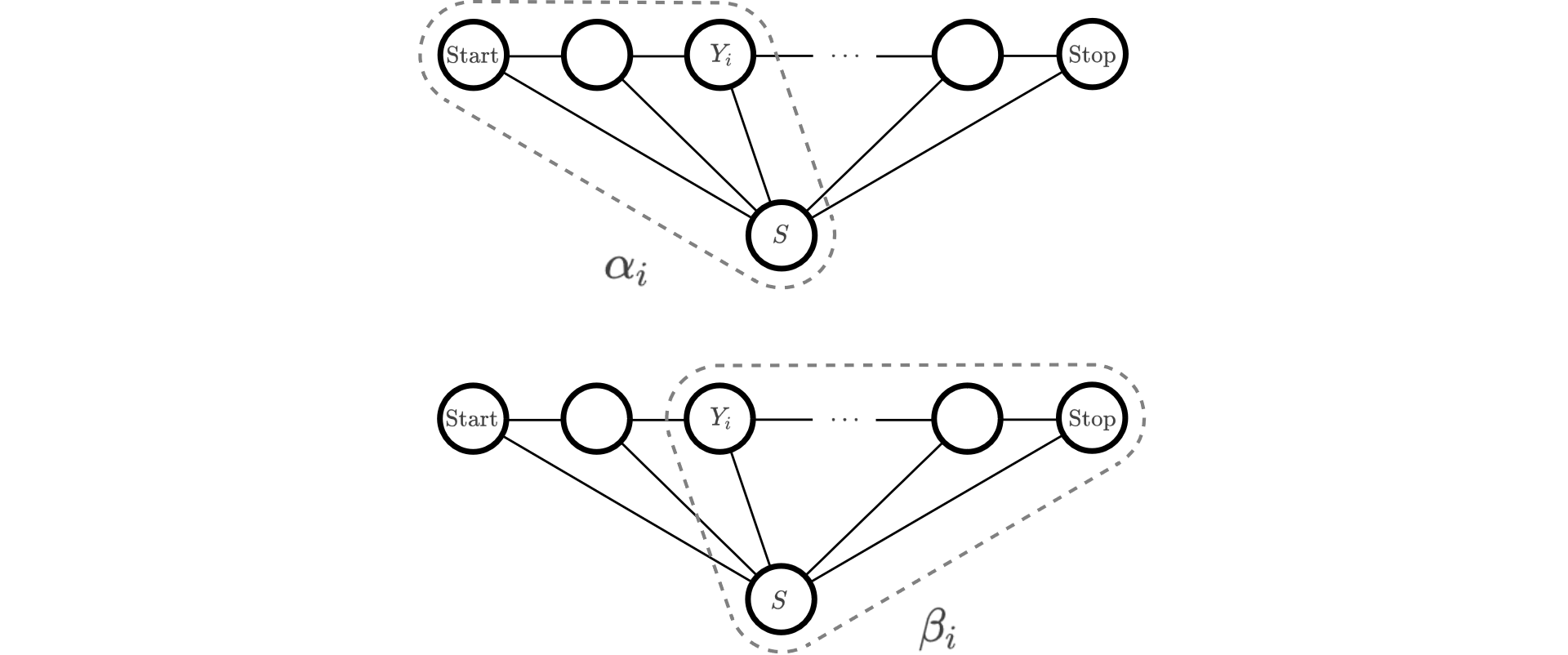
我们可以看到 $\alpha_i$ 是在前部分子图上求未归一化概率 $\tilde{P}(Y_i,S)$,而 $\beta_i$ 是在后部分子图上求未归一化概率 $\tilde{P}(Y_i,S)$
预测问题
条件随机场中的解码问题的解决方法与隐马尔可夫模型中的解法基本上是一致的,都是使用了维比特算法
\[\begin{split} Y^\star&=\mathop{\text{argmax}}_{Y}P(Y|S)\\ &=\mathop{\text{argmax}}_{Y}\frac{1}{Z(S)}\tilde{P}(Y,S)\\ &=\mathop{\text{argmax}}_{Y}\tilde{P}(Y,S)\\ &=\mathop{\text{argmax}}_{Y}\prod_{i=1}^{n+1}\phi(Y_i,Y_{i-1},S)\\ &=\mathop{\text{argmax}}_{Y}\prod_{i=1}^{n+1}\exp(\mathop{\mathcal{Score}}(S,i,Y_{i-1},Y_i))\\ &=\mathop{\text{argmax}}_{Y}\exp(\sum_{i=1}^{n+1}\mathop{\mathcal{Score}}(S,i,Y_{i-1},Y_i))\\ &=\mathop{\text{argmax}}_{Y}\sum_{i=1}^{n+1}\mathop{\mathcal{Score}}(S,i,Y_{i-1},Y_i)\\ &=\mathop{\text{argmax}}_{Y}\sum_{i=1}^{n+1}\boldsymbol{w}\cdot \boldsymbol{f}(S,i,Y_{i-1},Y_i)\\ \end{split}\]-
初始值
\[\delta_1 = \boldsymbol{w}\cdot \boldsymbol{f}(S,1,Y_1,\text{Start})\\\] -
递推 对 $i = 2,3,\dotsc,n$
\[\delta_i = \max_{Y_{i-1}}\left(\delta_{i-1} + \boldsymbol{w}\cdot \boldsymbol{f}(S,i,Y_{i-1},Y_i)\right) \\ \varPsi_i = \mathop{\text{argmax}}_{Y_{i-1}}\left(\delta_{i-1} + \boldsymbol{w}\cdot \boldsymbol{f}(S,i,Y_{i-1},Y_i)\right)\\\] -
结束
\[\max_{Y}P(Y|S) = \max_{Y_n}\delta_{n}\\ Y_n^\star=\mathop{\text{argmax}}_{Y_n}\delta_{n}\] -
最优路径回溯 对 $i = n-1,n-2,\dotsc,1$
\[Y_i^\star=\varPsi_{i+1}(Y_{i+1}^*)\]
对此我们可以得到最优的词性标注序列 $Y^\star={Y_1^\star,Y_2^\star,\dotsc,Y_n^\star}$
学习问题
由于在条件随机场中使用了全局归一化常数 $Z(S)$ 导致参数高度耦合,因此我们没法得到解析解,但是因此目标函数是凹的2,我们可以使用迭代方法来获取最优解。
学习过程中,我们希望有 $N$ 个训练数据的训练数据集 $\mathcal{D}$ 中所有数据对 $(S^j,Y^j)$ 的条件概率 $P(S=S^j|Y=Y^j)$ 最大化,于是我们给出条件随机场的最大似然函数
接下来我们对最大似然函数对权重 $\boldsymbol{w}$ 进行求导
\[\begin{split} \frac{\partial \mathcal{LL}(\mathcal{D};\boldsymbol{w})}{\partial \boldsymbol{w}} &= \sum_{j=1}^N\left(\frac{\partial\left(\sum_{i=1}^{n+1}\boldsymbol{w}\cdot \boldsymbol{f}\left(S=S^j,i,Y_{i-1}=y_{i-1}^j,Y_i=y_i^j\right)\right)}{\partial \boldsymbol{w}}-\frac{\partial\log Z(S=S^j)}{\partial \boldsymbol{w}}\right)\\ &=\sum_{j=1}^N\left(\sum_{i=1}^{n+1}\boldsymbol{f}\left(S=S^j,i,Y_{i-1}=y_{i-1}^j,Y_i=y_i^j\right) - \frac{\partial\log Z(S=S^j)}{\partial \boldsymbol{w}}\right)\\ \end{split}\]其中 $\frac{\partial\log Z(S)}{\partial \boldsymbol{w}}$ 为
\[\begin{split} \frac{\partial\log Z(S)}{\partial \boldsymbol{w}} &= \frac{Z'(S)}{Z(S)}\\ &=\frac{1}{Z(S)}\sum_{Y_1,Y_2,\dotsc,Y_n}\left(\prod_{i=1}^{n+1}\exp\left(\boldsymbol{w}\cdot \boldsymbol{f}\left(S,i,Y_{i-1},Y_i\right)\right)\right)'\\ &=\frac{1}{Z(S)}\sum_{Y_1,Y_2,\dotsc,Y_n}\left(\exp\left(\sum_{i=1}^{n+1}\boldsymbol{w}\cdot \boldsymbol{f}\left(S,i,Y_{i-1},Y_i\right)\right)\right)'\\ &=\frac{1}{Z(S)}\sum_{Y_1,Y_2,\dotsc,Y_n}\left(\exp\left(\sum_{i=1}^{n+1}\boldsymbol{w}\cdot \boldsymbol{f}\left(S,i,Y_{i-1},Y_i\right)\right)\sum_{i=1}^{n+1}\boldsymbol{f}\left(S,i,Y_{i-1},Y_i\right)\right)\\ &=\sum_{Y_1,Y_2,\dotsc,Y_n}\left(\frac{P(Y,S)}{Z(S)}\sum_{i=1}^{n+1}\boldsymbol{f}\left(S,i,Y_{i-1},Y_i\right)\right)\\ &=\sum_{Y_1,Y_2,\dotsc,Y_n}\left(P(Y|S)\sum_{i=1}^{n+1}\boldsymbol{f}\left(S,i,Y_{i-1},Y_i\right)\right)\\ &=\sum_{i=1}^{n+1}\sum_{Y_1,Y_2,\dotsc,Y_n}P(Y|S)\boldsymbol{f}\left(S,i,Y_{i-1},Y_i\right)\\ &=\sum_{i=1}^{n+1}\sum_{Y_{i-1},Y_i}\left(\boldsymbol{f}\left(S,i,Y_{i-1},Y_i\right)\sum_{Y_{\neq\{i,i-1\}}}P(Y|S)\right)\\ &=\sum_{i=1}^{n+1}\sum_{Y_{i-1},Y_i}\boldsymbol{f}\left(S,i,Y_{i-1},Y_i\right)P(Y_{i-1},Y_i|S)\\ \end{split}\]最后我们有
\[\begin{split} \frac{\partial \mathcal{LL}(\mathcal{D};\boldsymbol{w})}{\partial \boldsymbol{w}} &=\sum_{j=1}^N\left(\sum_{i=1}^{n+1}\boldsymbol{f}\left(S=S^j,i,Y_{i-1}=y_{i-1}^j,Y_i=y_i^j\right) - \sum_{i=1}^{n+1}\sum_{Y_{i-1},Y_i}\boldsymbol{f}\left(S,i,Y_{i-1},Y_i\right)P\left(Y_{i-1},Y_i|S\right)\right)\\ &=\sum_{j=1}^N\sum_{i=1}^{n+1}\left(\boldsymbol{f}\left(S=S^j,i,Y_{i-1}=y_{i-1}^j,Y_i=y_i^j\right) - \sum_{Y_{i-1},Y_i}\boldsymbol{f}\left(S=S^j,i,Y_{i-1},Y_i\right)P\left(Y_{i-1},Y_i|S=S^j\right)\right) \end{split}\]我们根据梯度使用优化算法就可以很快,迭代出最优的权重 $\boldsymbol{w}$ 了。
最后
在写这篇文章的时候,再次将涉及到的公式推导了一遍,算是重新温习了一下HMM和CRF,其中发现了许多第一次学习这两个模型时候忽略的东西,比如HMM向前和向后算法中所表达的物理含义是不同的。还有写博客真的好累,尤其是画图的时候。
